Sinewave Addition in Tables

One can also add sine waves together (additive synthesis) to approximate the basic forms presented earlier in this section. Individual sine waves of appropriate frequencies and amplitudes (with matching phases) can be used or one can use a lookup method and fill the table with the sum of the waves. The latter method is shown here.

Sawtooth and Ramp

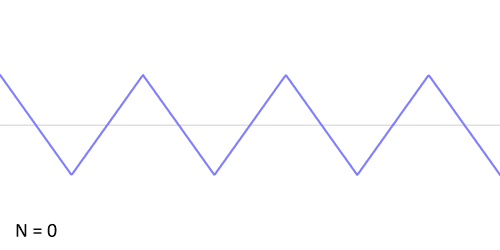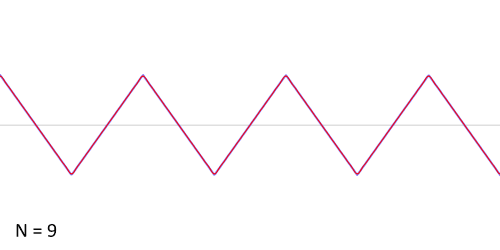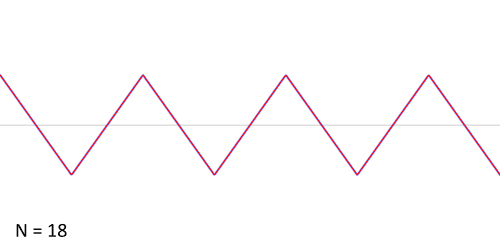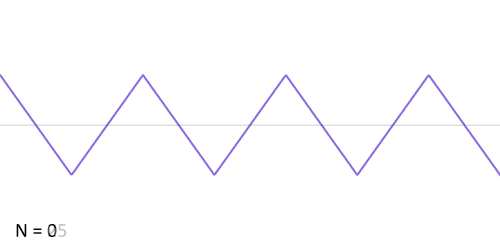
The sawtooth has perhaps the most simple formula: given a harmonic series of sine waves, multiply each by the reciprocal of their harmonic number and sum. For instance, the first harmonic is multiplied by 1/1, the second harmonic, is multiplied by 1/2, the third harmonic is multiplied by 1/3, and so on. In other words:

 x_{saw}(t) = \sum_{i=1}^{k} \frac{1}{k} sin(2\pi fkt)

where k is the number of harmonics and sin(2πfkt) is a sine wave.

float table[1024];
int harmonics = 10; // 10 harmonics
float amp = 1.0; // amplitude
float max = 0; // for normalization

// clear the table
for(i=0; i < tableSize; i++) '
   table[i] = 0.0;

// fill the table
for(k=1; k <= harmonics; k++) 
{
    // for each harmonic, go through and add it to the table
    for(i=0; i < tableSize; i++) 
    {
        float samp;
        samp = (i*k)/tableSize; // get the increment
        samp = samp * 2PI; // scale the frequency
        table[i] = table[i] + (sin(samp) * 1/harmonic); // add it
        if (table[i] > max)
            max = table[i]; // remember it if it's the largest value we've encountere
    }
}

// normalize
for(i=0; i < tableSize; i++)
   table[i] = table[i]/max; // scale

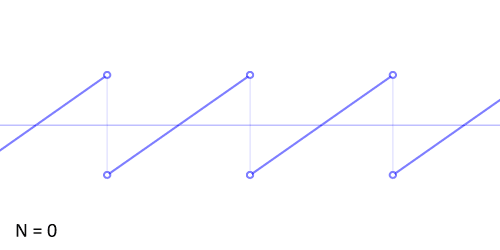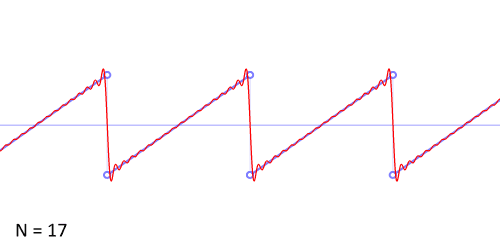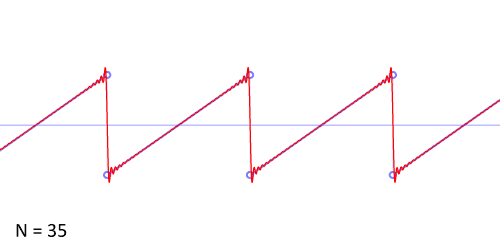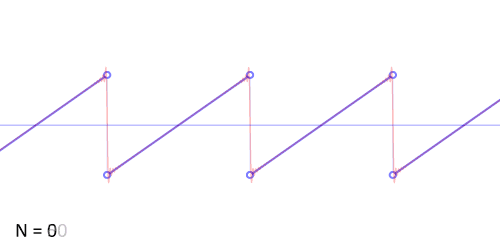
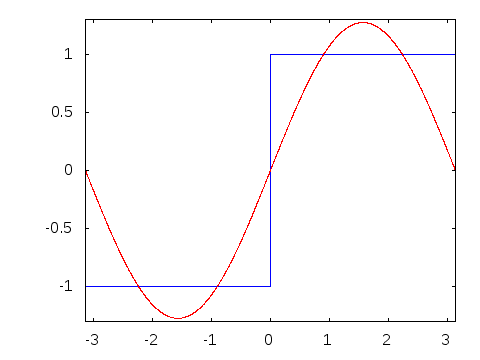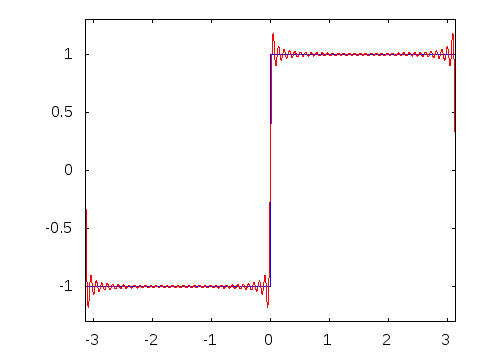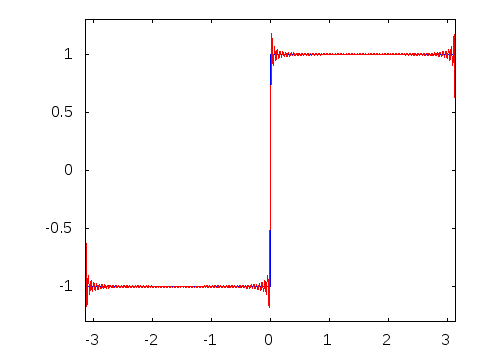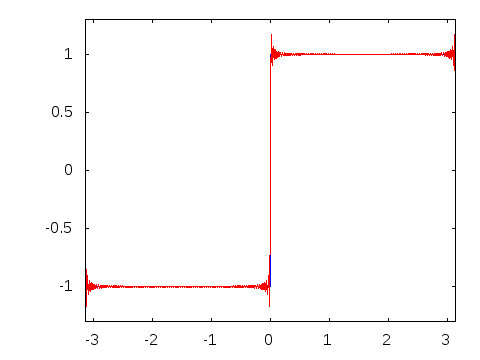
The following is an animation of the process. N is the number of harmonics used to construct the wave. Notice that as N increases, the result is increasingly sharp and similar to an algebraically constructed sawtooth.

Ramp

The ramp is created by simply inverting the phase of the sine wave used in the sawtooth:

 x_{ramp}(t) = \sum_{i=1}^{k} \frac{-1}{k} sin(2\pi fkt)

Square

The square wave is created in much the same way as the sawtooth but using only the odd-numbered harmonics:

x_{square}(t) = \sum_{i=1}^{2k+1} \frac{1}{k} sin(2\pi fkt)

float table[1024];
int harmonics = 10; // 10 harmonics
float amp = 1.0; // amplitude
float max = 0; // for normalization

for(i=0; i<tableSize; i++)
    table[i] = 0.0;
// fill the table
for(k=1; k <= harmonics; k++) 
{
   // if the harmonic is odd, go through and add it to the table
   if (k & 1 == 1) 
   {
      for(i=0; i < tableSize; i++) 
      {
          float samp;
          samp = (i*k)/tableSize; // get the increment
          samp = samp * 2PI; // scale the frequency
          table[i] = table[i] + (sin(samp) * 1/harmonic); // add it
          if (table[i] > max)
              max = table[i]; // remember it if it's the largest value we've encountered
      }
   }
}

// normalize
for(i=0; i < tableSize; i++)
    table[i] = table[i]/max; // scale

Notice that in the same way as the sawtooth, when we increase the number of harmonics of the square wave we more closely resemble an algebraically constructed one.

Triangle

The triangle wave, like the square wave, uses only odd harmonics but the phase of every other harmonic is inverted (multiplied by -1 or phase change by π). The amplitude of the harmonics, however, is the reciprocal of the square of their mode number. This means that the first harmonic is multiplied by 1/1², the third harmonic is multiplied by 1/3², the fifth by 1/5², etc.

x_{triangle}(t) = \sum_{i=1}^{k} (-1)^{i} n^{-2} (\text{sin}[nt])

float table[1024];
int harmonics = 10; // 10 harmonics
float amp = 1.0; // amplitude
float max = 0; // for normalization
boolean invertPhase = false; // boolean to invert the phase

for(i=0; i<tableSize; i++)
    table[i] = 0.0;

//fill the table 
for(k=1; k <= harmonics; k++) 
{ 
    // if the harmonic is odd, go through and add it to the table 
    if (k & 1 == 1) 
    { 
        for(i=0; i < tableSize; i++) 
        { 
            float samp; 
            samp = (i*k)/tableSize; // get the increment 
            samp = samp * 2PI; 
            // scale the frequency 
            table[i] = table[i] + (sin(samp) * 1/(harmonic**2)); 
            // add it 
            if (invertPhase) 
            { 
                table[i] = -1 * table[i]; // invert the phase 
                invertPhase = false; // don't invert next time 
            } 
            else 
                invertPhase = true; // invert the next time 
            if (table[i] > max)
                max = table[i]; // remember it if it's the largest value we've encountered for normalization 
         }
     } 
}

// normalize 
for(i=0; i < tableSize; i++)
    table[i] = table[i]/max; // scale

Notice that in the same way as the sawtooth, when we increase the number of harmonics of the triangle wave we more closely resemble an algebraically constructed one.

Addition using individual Sinewaves

In the same way we can populate a table to create a waveform, one can also generate and add the same sine tones individually and sum them in the output. The technique is to essentially calculate the relative amplitudes using the same formulas as before, put them in a table, and read from them during playback.

float frequency = 440; // fundamental in Hz
int harms = 10; // number of harmonics
float phase;
float harmonicAmp[harms+1]; // a table to keep the amplitudes in

// define a function to calculate the amplitudes
double sawtoothAmp(int harm) 
{
    return(1.0/(double)harm);
}

// populate the table of amplitudes
for(i=1; i <= harms; i++) {
  harmonicAmp[i] = sawtoothAmp(i);
}

// calculate a block
for(sample = 0; sample < samples; sample++)
{
    // the phase increment is linearly
    // related to sample rate
    phase += (frequency * 6.28318531)/samplerate; 
    sawtooth = 0.0;
    for(harm = 1; harm <= harms; harm++)
        sawtooth += sin(phase * harm) * harmonicAmp[harm];
    output[sample] = sawtooth;
}

Using this technique, one could also address the amplitude of each harmonic individually after the waveform has been created. This could allow one to blend waveforms in time.