Frequency Modulation is a synthesis technique that all should be familiar with. FM synthesis was invented by John Chowning in 1968, and subsequently the most commercially popular digital synthesis method. It involves at least 2 operators (sine oscillator with amplifier), in which one is the modulator and the other is the carrier (the operator being modulated, as well as the one that is heard).
The theory of FM synthesis can be found in Chowning’s article “The Synthesis of Complex Audio Spectra by Means of Frequency Modulation”. Breifly, frequency modulation acts somewhat like amplitude modulation in that upper and lower sidebands are created around the carrier frequency. These sidebands are separated from the frequency of the carrier by the frequency of the modulator, so that they appear at f_{car} + f_{mod} and f_{car} - f_{mod}. What separates FM from AM is that additional sidebands appear at multiples of the modulator frequency, and increased depth of modulation increases the strength of higher sidebands. Also when f_{car} - n*f_{mod} drops below 0Hz, it reflects around 0Hz with a phase inversion. As with AM, a simple harmonic relation between the carrier and modulator will create a more consonant sound Finally, multiple carriers and modulators can be used to specify a spectrum in more detail, and modulation feedback can be used to create noise and chaotic oscillation..
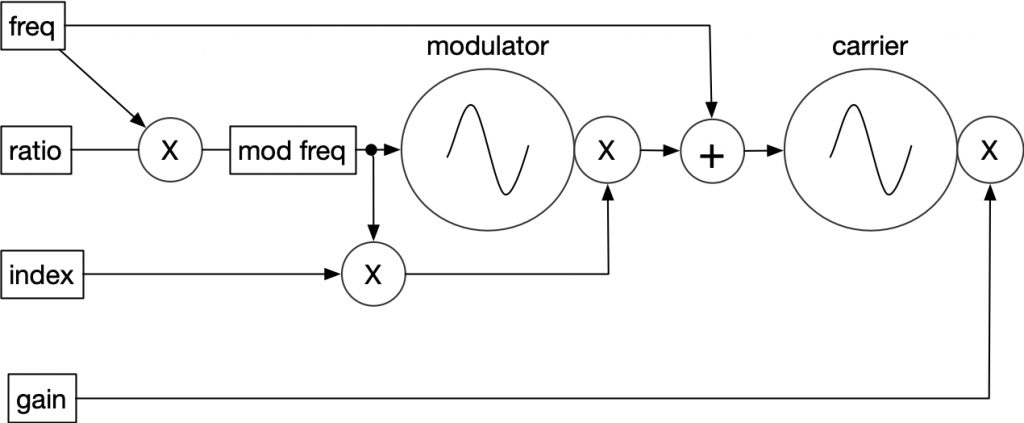
Implementation
One of the attractive aspects of two operator FM synthesis is that this very straightforward and seemingly simple structure can intuitively create many timbres. The index parameter acts very much like a brightness control, a ratio of 1 will synthesize all harmonics, a ratio of 2 will create odd harmonics, and higher ratios further separate the overtones. The only limit to index and ratio is the Nyquist frequency.
In C, two table lookup oscillators are used. In practice, interpolation would be used in these oscillators to reduce quantization noise.
// the samplerate in Hz
float sampleRate = 44100;
// initial phase
float phaseCar = 0.0;
float phaseMod = 0.0;
long tableSize = 8192;
long tableMask = 8191;
float sineTab[8192];
void InitTables(void)
{
// create sineTab from sin()
for(i = 0; i < tableSize; i++)
{
sineTab[i] = sin((6.283185307179586 * i)/tableSize);
}
}
void TwoOpFM(float *input, float *output, float frequency, float ratio, float index, float gain, long samples)
{
long sample;
float phaseIncCar, phaseIncMod;
float carrier, modulator;
// calculate for each sample in a block
for(sample = 0; sample < samples; sample++)
{
// get the phase increment for this sample
// frequency of modulator is frequency of carrier * ratio
phaseIncMod = (frequency * ratio)/sampleRate;
// calculate the waveforms
modulator = sineTab[(long)(phaseMod * tableSize)];
phaseIncCar = (frequency + (modulator * frequency * ratio * index))/sampleRate;
carrier = sineTab[(long)(phaseCar * tableSize)];
*(output+sample) = carrier * gain;
// increment the phases
phaseMod = phaseMod + phaseModInc;
phaseCar = phaseCar + phaseIncCar;
if(phaseMod >= 1.0)
phaseMod = phaseMod - 1.0;
// phaseCar can get large fast and can go negative
// must be kept between 0 and 1
while(phaseCar >= 1.0)
phaseCar = phaseCar - 1.0;
while(phaseCar < 0.0)
phaseCar = phaseCar + 1.0;
}
}
Multiple Carriers, Feedback FM and further
One could easily add more to this simple network. One of the common additions is that of a second carrier with it’s own index of modulation. This can be used to simulate formants, or increase upper harmonics without increasing middle harmonics.
Feedback is often used in small amounts to create a bit of noise for the attack of the note. This can be done by adding a modulation path from the carrier to the modulator. There will be an additional sample delay in this feedback, but this technique can create a wide variety of noise depending on the index and frequency.
Finally, there are many, many papers on synthesis with FM, as well as commercial instruments that have some very expressive FM patches. It is well worth it to study these patches and techniques.