Complex Sinusoids

Complex sinusoids are two-dimensional signals whose value at any instant can be specified by a complex number; that is, a number with real part and an imaginary part. These two parts are in what is known as phase quadrature with one another; i.e. the imaginary part is pi/2 radians out of phase with the real part (1/4 of a cycle). That is why the components of the complex signal are sometimes known as in-phase and quadrature phase.

A complex sinusoid is defined by the following mathematical representations:

Cartesian Form:
x(t) \triangleq Acos(\omega t + \phi) + jAsin(\omega t + \phi)

Polar Form:
(t) = Ae^{j(\omega t + \phi)}

where A is amplitude, ω is the angular frequency in radians per second (the frequency in Hertz scaled by 2π; 2πf), ϕ is the initial phase offset in radians, and t is time in seconds. The cosine portion of the sinusoid is the real component and the sine portion is the imaginary (phase quadrature) component. (In engineering, the variable j is typically denoted to mean the square root of negative 1, whereas pure math often uses the variable i to mean the same thing).

Projection

Recall the Pythagorean Identity:
cos^2(\phi) + sin^2(\phi) = 1

Reconfiguring the Cartesian form of a complex sinusoid with this in mind, we get:
|x(t)| \triangleq \sqrt{re^2\{x(t)\} + im\{x(t)\}} \equiv A

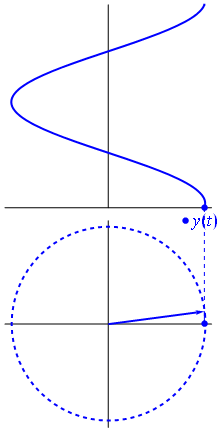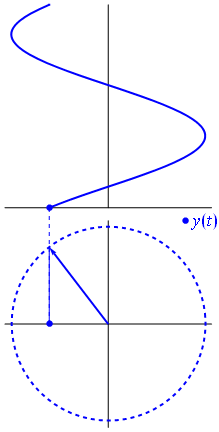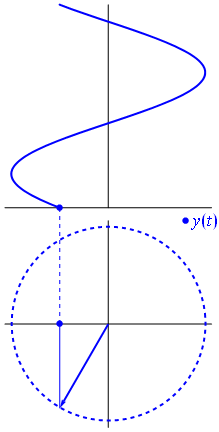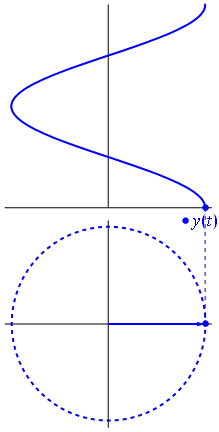
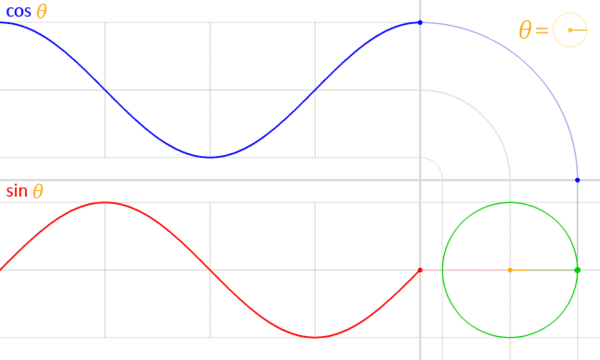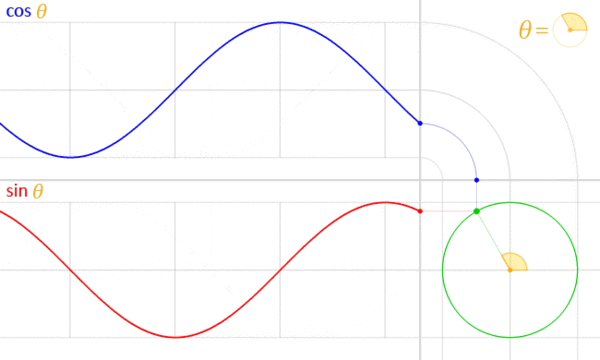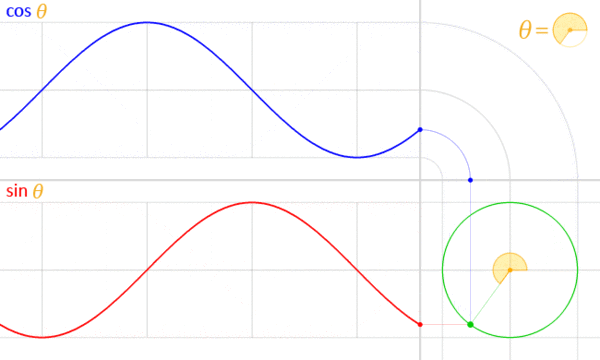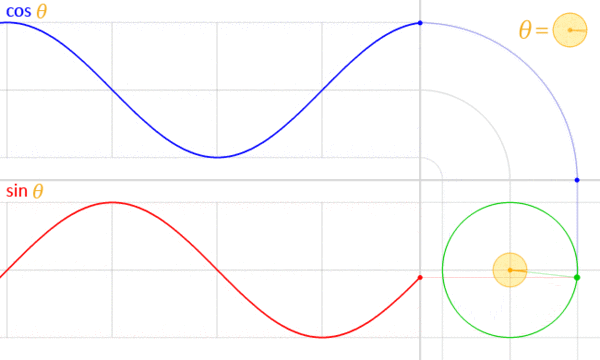
In other words, a complex sinusoid has a constant complex magnitude (A). Since this is true, the projection of a complex signal (in complex form) onto the complex plane must lie on a circle; i.e. the radius (magnitude) remains the same while the angle changes). Recall the animation in the beginning of this section:

This animation shows the counter-clockwise motion of the real (cosine) component of the complex sinusoid projected onto the complex plane. We can also project the complex phasor onto orthogonal axes:

The green circle in the bottom right corner is the unit circle in the complex plane. We can rewrite the trigonometric form of the equation into polar form:
cos\theta + jsin\theta = re^{j\theta}

where j is the square root of negative 1, r is the length (or magnitude), θ is the angle in radians, and e is Euler’s number.

Relabeling a sine wave:

Advantages

Representing a sinewave in complex form has several distinct advantages:

Instantaneous Frequency:
f = \omega + \frac{d}{dt}\phi(t)

Instantaneous Phase:
\angle x(t) = \omega t + \phi

Instantaneous Magnitude (Amplitude):
A = \sqrt{re^2\{x(t)\} + im\{x(t)\}}

Using complex sinusoid generation in an oscillator

This method of calculation can be used for a fairly efficient sine and cosine wave generator. The only CPU intensive calculation is the calculation of the complex phase factor. If using a limited set of frequencies, the complex phase could be pre-calculated in a table.

double cosZ, sinZ;

SinComplex(float freq, float *output, long samplesPerBlock)
{
	long sample;
	float freqAngle, angleReal, angleImag;
	
	freqAngle = twoPi * freq;
        // calculate the phose angle for given frequency
	angleReal = cos(freqAngle);
	angleImag = sin(freqAngle);
	for(sample = 0; sample<samplesPerBlock; sample++) 	
        { 		
            // complex multiply by phase angle for sin output
            *(output+sample) = angleReal * sinZ - angleImag * cosZ;
            // complex multiply by phase angle for cos output
            cosZ = angleReal * cosZ + angleImag * sinZ; 
            sinZ = *(output+sample); 
            // correction for accumulated computation inaccuracies
            if(sinZ < -1.0) sinZ = -1.0;
            if(sinZ > 1.0f) sinZ = 1.0f; 
        } 
}