The chebyshev polynomials are often used in synthesis to create harmonics from sinusoidal components. Five of the polynomials (degree 2 to 6) are plotted below:
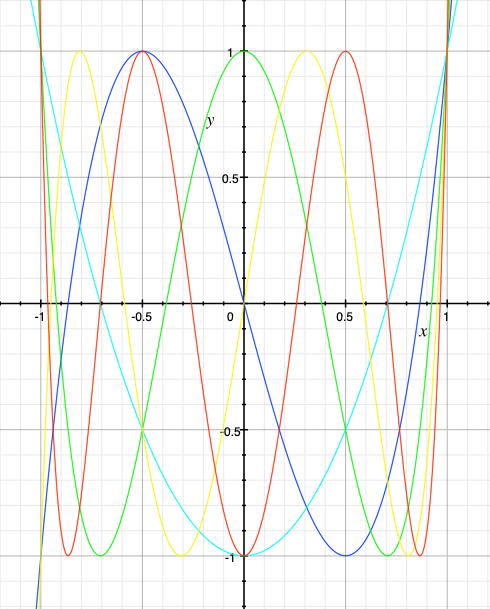
degree 2 (light blue): y = 2x^2 - 1
degree3 (blue): y = 4x^3 - 3x
degree 4 (green): y = 8x^4 - 8x^2 + 1
degree 5 (yellow): y = 16x^5 - 20x^3 + 5x
degree 6 (red): y = 32x^6 - 48x^4 + 18x^2 - 1
These transfer functions are used for input signals within the range of -1 to 1, as the output of these functions rapidly increase beyond that. The gain on the input signal should be limited to 1.0. Because of the curved reversals in the chebyshev polynomials, they can be used as smooth wavefolders. As the input signal increases, the output quickly goes to the maximum value and wraps back. This smoothed wavefolding creates higher harmonics based on the original harmonics.
Furthermore, the chebyshev polynomials have an interesting effect on sine waves. When the sine wave is at a low level, the degree 3 polynomial will reproduce the sine wave, as the sine wave increases in volume, the 3rd harmonic will appear, and at full volume, the fundamental will disappear.
| degree | harmonic transformation |
|---|---|
| 2 | 0 – 2 |
| 3 | 1 – 3 |
| 4 | 0 – 2 – 4 |
| 5 | 1 – 3 – 5 |
| 6 | 0 – 2 – 4 – 6 |
One should note that if these are applied to harmonically rich waveforms or samples, every harmonic in the source signal will be multiplied. In this context, these waveshapers will create harmonic distortion and sound much like a distorted amplifier. Also, the even polynomials contain a DC component (harmonic 0). For practical use it may be necessary to remove the DC offset with a high pass filter.
When working with sine waves, the chebyshev waveshapers can be very effectively used for direct harmonic synthesis. They can also be used to replace the sine wave oscillators in additive synthesis or frequency modulation to extend those synthesis techniques.
