With a frequency tunable allpass filter, it is simple to create both low pass and high pass filters. As the first order allpass has a phase shift of π at the nyquist frequency and a phase shift of zero at 0 Hz, it can be added to the input to create a lowpass filter. To maintain the same amplitude at 0 Hz, the output is multiplied by 1/2. The following C code show this slight modification to the first order allpass filter.

double in1 = 0; // delayed sample
double out = 0; // keep track of the last output

folp(float *input, float *output, long samples, float cutoff) 
{
    double tf = tan(PI * (cutoff/SAMPLERATE)); // tangent frequency
    double c = (tf - 1.0)/(tf + 1.0); // coefficient

    for(int i = 0; i < samples; i++) 
    {
        double sample = *(input+i);
        out = (c*sample) + in1 - (c * out); // get the output
        in1 = sample; // remember it
        *(output+i) = (sample+out)*0.5; 
       // add and scale to get lowpass
  }
}

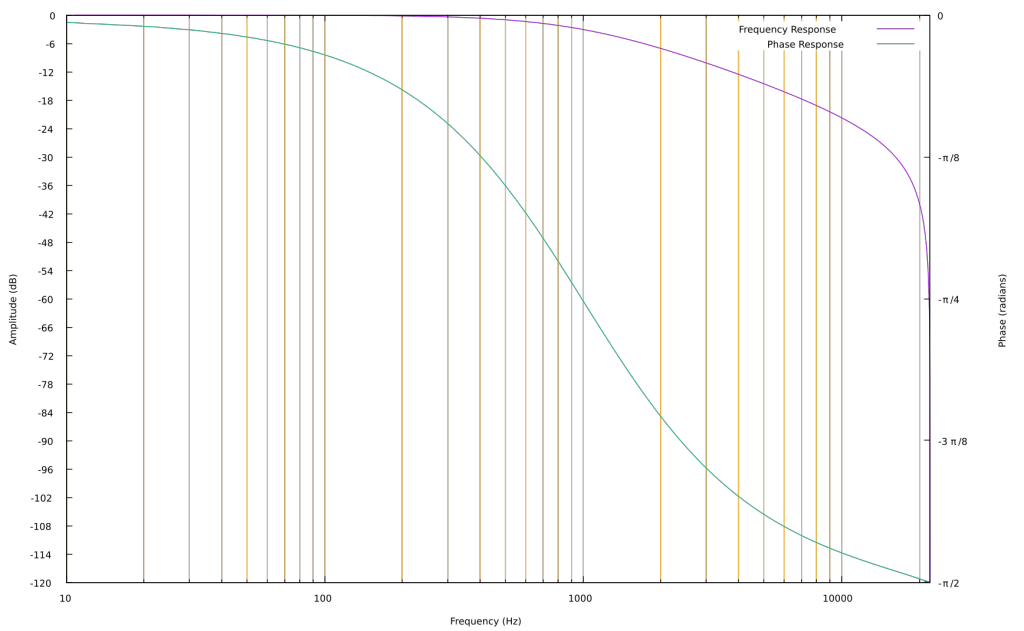
At the cutoff frequency, there will be a phase shift of π/2 (90 degrees) at the output of the allpass. When we add the input to the allpass output, we will have a combined phase shift of (π/4) and a gain equal to half the hypotenuse of 1 and 1 – or 0.70710678. This gain is approximately -3 dB. This graph shows the gain and phase shift of a low pass filter set to 1000Hz.

A first order highpass is almost identical to the lowpass except the allpass output is subtracted from the input.

double in1 = 0; // delayed sample
double out = 0; // keep track of the last output

fohp(float *input, float *output, long samples, float cutoff) 
{
    double tf = tan(PI * (cutoff/SAMPLERATE)); // tangent frequency
    double c = (tf - 1.0)/(tf + 1.0); // coefficient

    for(int i = 0; i < samples; i++) 
    {
        double sample = *(input+i);
        out = (c*sample) + in1 - (c * out); // get the output
        in1 = sample; // remember it
        *(output+i) = (sample-out)*0.5; 
       // add and scale to get highpass
  }
}