The Phasor

The phasor is perhaps the most simple and fundamental of oscillators. It takes the shape of a sawtooth wave but has two important differences:

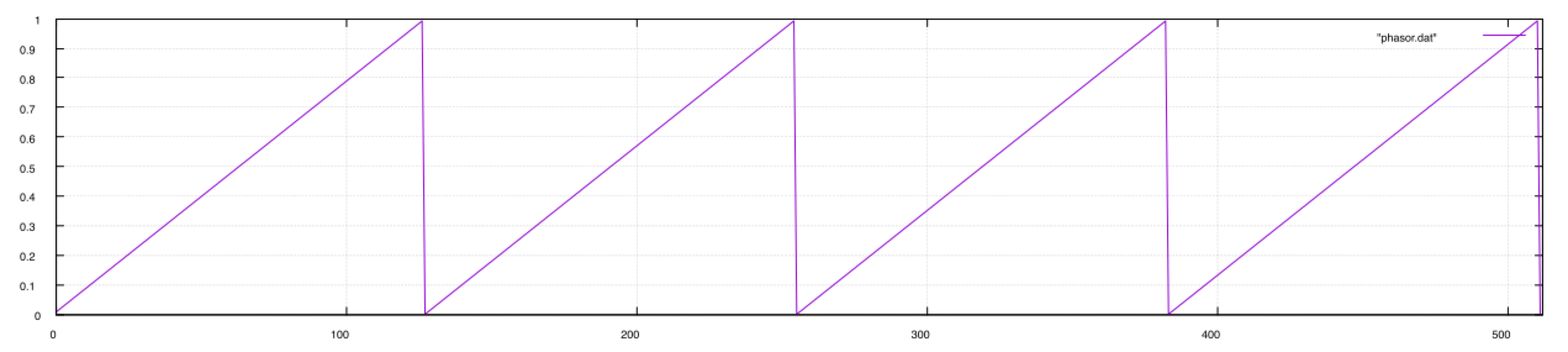
1. It ascends from 0 to 1, as opposed from -1 to +1.
2. It is _not_ bandlimited (in discrete time this matters).

where p is the period in Hertz and t is time.

sampleRate = 128;    // the samplerate in Hz
freq = 1;            // the frequency in Hz
phasePerSecond = freq;  // the change in phase per unit of time; 
                        // i.e. the frequency when time is seconds
phasePerSample = freq/sampleRate;   // the amount of change in phase per 
                                    // sample for a given frequency at a 
                                    // given samplerate
Osc::Osc()
{
    phase = 0.0;
    phasePerSample = 0.0;
}

void Osc::Phasor(float frequency, float *output, long samplesPerBlock)
{
    long sample;
    // calculate for each sample in a block
    for(sample = 0; sample<samplesPerBlock; sample++)
    {
        phasePerSample = frequency/sampleRate; // get the phase increment for this sample
        *(output+sample) = phase; // calculate the output for this sample
        phase = phase + phasePerSample; // increment the phase
    }
}

Important here is the relationship between `phasePerSample` and `freq`: they are, in fact, representations of the same thing. With frequency, we give the total number of rotations (oscillations) in a second while phase per sample is the rate of change at the sampling period. If we want to give an oscillator a frequency, we will need to calculate the change in phase per sample; i.e. `phasePerSample`.

Using a samplerate of 128Hz, the first 512 samples of a 1Hz phasor are plotted below:

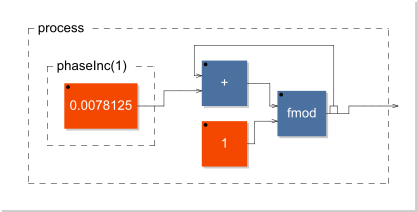
Notice how the waveform ascends from 0 to 1 as noted above. This makes it extraordinarily useful in waveshaping, indexing into tables, etc. As a simplified block diagram, the phasor looks like this:

`phaseInc(1)` is the phase increment for a 1Hz signal at a 128Hz samplerate. 1/128 = 0.0078125.